Compilers-PA3

发表于 分类于 阅读数： 评论数： 本文字数： 4.8k 阅读时长 ≈ 8 分钟
The solution of Programming Assignment III for CS143(Stanford).

Introduction

In this assignment you will write a parser for Cool.The assignment makes use of two tools: the parser generator (the C++ tool is called bison) and a package for manipulating trees. The output of your parser will be an abstract syntax tree (AST). You will construct this AST using semantic actions of the parser generator.

Analysis and Solution

First of all, We need to declare bison “types” for our non-terminals that have attributes.

1
2
3
4
5
6
7
8
9
10
11
12
13
%type <program> program
%type <classes> class_list
%type <class_> class
%type <features> feature_list
%type <feature> feature
%type <formals> formal_list
%type <formal> formal
%type <cases> case_list
%type <case_> case 
%type <expressions> expr_list_semi
%type <expressions> expr_list_comma
%type <expression>  expr
%type <expression> let_nested

It is critical that you declare the correct types for the attributes of grammar symbols; failure to do so virtually guarantees that your parser won’t work.

Then we will declare the operator precedence in cool-lang.

The precedence of infix binary and prefix unary operations, from highest to lowest, is given by the following table:

1
2
3
4
5
6
7
8
9
.
@
~
isvoid
* /
+ -
<= < =
not
<-

All binary operations are left-associative, with the exception of assignment, which is right-associative, and the three comparison operations, which do not associate.[1]

Transform them into bison rules.

1
2
3
4
5
6
7
8
9
%right ASSIGN
%left NOT
%nonassoc LE '<' '='
%left '-' '+'
%left '/' '*'
%left ISVOID
%left '~'
%left '@'
%left '.'

The associativity of an operator op determines how repeated uses of the operator nest: whether ‘x op y op z’ is parsed by grouping x with y first or by grouping y with z first. %left specifies left-associativity (grouping x with y first) and %right specifies right-associativity (grouping y with z first). %nonassoc specifies no associativity, which means that ‘x op y op z’ is considered a syntax error.[2]

The Bison declarations has been completed, and now we will start coding the grammar rules.

The regular expressions are provided in the cool manual.[3]

In order to coding grammar rules, we need to those prototypes of the interface in cool-tree.h

The function nil phylums() returns an empty list of type phylum. The function single phylums makes a list of length 1 out of its phylum argument. The function append phylums appends two lists of phylums. The method nth selects the index’th element of its list argument. The method len returns the length of the list.[4]

The other functions can also be referenced in the cool-tour.[5]

According to ‘Figure 1: Cool syntax’, the feature_list can be empty, indicating that there are no features or the feature_list can also consist of multiple features, each followed by a semicolon.

1
2
3
4
5
6
7
8
9
10
11
12
13
feature_list
                  : /* empty */ {  $$ = nil_Features(); }
                  | feature_list feature ';' { $$ = append_Features($1,single_Features($2)); }
                  | feature ';'  { $$ = single_Features($1); }
                  | feature_list error ';' { $$ = $1; }
                  | error ';' {  $$ = nil_Features(); }
                  ;

    feature
            : OBJECTID '(' formal_list ')' ':' TYPEID '{' expr '}'  { $$ = method($1,$3,$6,$8); }
            | OBJECTID ':' TYPEID ASSIGN expr  { $$ = attr($1,$3,$5); }
            | OBJECTID ':' TYPEID  { $$ = attr($1,$3,no_expr()); }
            ;

Here are two special cases:

According to ‘Figure 1: Cool syntax,’ a comma or semicolon can follow an expr. As a result, we will declare two non-terminals: expr_list_comma and expr_list_semi.

1
2
3
4
5
6
7
8
9
10
11
12
expr_list_comma
                    : expr_list_comma ',' expr { $$ = append_Expressions($1,single_Expressions($3)); }
                    | expr  { $$ = single_Expressions($1); }
                    | /* empty */ { $$ = nil_Expressions(); }
                    ;

    expr_list_semi
                    : expr ';'  { $$ = single_Expressions($1); }
                    | expr_list_semi expr ';' { $$ = append_Expressions($1,single_Expressions($2)); }
                    | expr_list_semi error ';' { $$ = $1; }
                    | error { $$ = nil_Expressions(); }
                    ;

A little challenging part is the nesting of let statements.

According to the cool-tour, when parsing a let expression with multiple identifiers, it should be transformed into nested lets with single identifiers.

for example :

1
let x : Int <- 10, y : String <- "Hello" in expression

It is considered as the following expression.

1
2
3
let x : Int <- 10 in
  let y : String <- "Hello" in
    expression

To address this, we can utilize recursive invocations of the let constructor.

1
2
3
4
5
6
7
let_nested
                : OBJECTID ':' TYPEID IN expr { $$ = let($1,$3,no_expr(),$5); }
                | OBJECTID ':' TYPEID ASSIGN expr IN expr { $$ = let($1,$3,$5,$7); }
                | OBJECTID ':' TYPEID ',' let_nested  { $$ = let($1,$3,no_expr(),$5); }
                | OBJECTID ':' TYPEID ASSIGN expr ',' let_nested  { $$ = let($1,$3,$5,$7); }
                | error ',' let_nested  { $$ = $3; }
                ;

The remaining code follows a conventional approach, reviewing the source code for yourself.

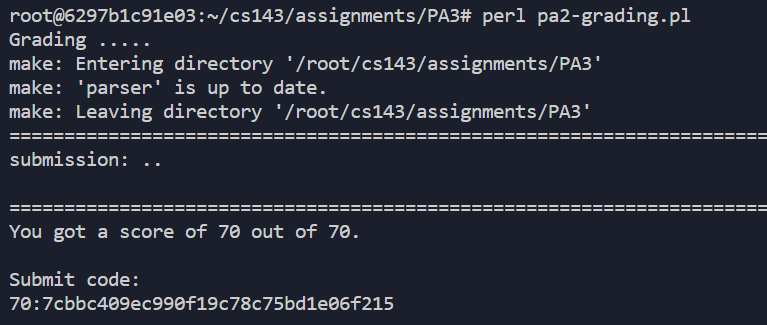
Result

SCORE 70/70

Here are all source code

  1. cool-manual p16 11.1 Precedence ↩︎

  2. bison-manual ↩︎

  3. cool-manual p16 12 Type Rules ↩︎

  4. cool-tour p5 6.2 AST Lists ↩︎

  5. cool-tour p6 6.5 The Constructors ↩︎