Compilers

发表于 分类于 阅读数： 评论数： 本文字数： 18k 阅读时长 ≈ 31 分钟
based on CS143(Stanford)

Introduction

Interpreters(online): program + data ==> output

Compilers(offline,run same executable on many different data): program==> exec + data ==> output

structure of a compiler

  1. llexical analysis

    dividing program text into “words” or “tokens”

  2. parsing

    digramming sentences

  3. semantic analysis

  4. optimization

  5. code generation

    translate a hign level program into assembly code

Lexical Analysis

the goals:

partition the input string into lexemes

identity the token of each lexeme

Token Class

identifier:strings of letters or digits,starting with a letter

integer:a non-epty string of digits

keyword:“else” or “if” or “begin” or…

whitespace:a non-epty sequence of blanks,newlines and tabs

and so on…

what’s more, “(”, “)” ,“;”… usually are the signle token class

string ==> (Lexical Analysis) ==> <token class,substring>(token) ==>parser

for instance: “foo=42” ==> <Id,“foo”> , <op,“=”> , <“Int”,42>

Lexical Specification

Regular expression grammar

At least one:===

Union: A|B === A+B

Option: A? ===A+ε

Range: ‘a’+‘b’+…+‘z’ === [a-z]

Complement of [a-z] === [^a-z]

how to design the lexical specification of a language ?

  1. Write a rexp for the lexemes of each token class

Number =

Keyword = ‘if’ + ‘else’ + …

Identifier =

OpenPar = ‘(’

and so on

  1. Construct R, matching all lexemes for all tokens

R = Keyword + Identifier + Number +…

  1. Assuming input be  

for 1 <= i <= n check  

  1. If success, then we konw that  

  2. Remove  from input and go to (3)

Parsing

PhaseInputOutput
LexerString of charactersString of tokens
ParserString of tokensParse tree

We need a language for describing vaild strings of tokens and a method for distinguishing valid from invaild strings of tokens because not all strings of tokens are programs

Derivations

A parse tree has terminals at leaves and non-terminals at the interior nodes

An in-order traversal of the leaves is the original input

Ambiguity

A grammer is ambiguous if it has more than one parse tree for some string

Serveral ways to handle ambiguity:

  1. rewriting grammar unambiguously

  2. enforcing precedence just like “*” has a higher precedence than “+”

Error Handling

Error handler should report errors accurately and clearly, recover from an error quickly and not slow down compilation of valid code.

Three kinds of error handling

Panic mode

When an error is detected, discard tokens until one with a clear role is found and continue from here

Looking for synchronizing tokens(Typically the statement or expression terminators)

for instance:

(1++2)+3

recovery: skip ahead to next integer and then continue

Error productions

specify known common mistakes in the grammar

disadvantage: complicates the grammar

for instance:

Write 5x instead of 5*x, add the production E -> …| EE

Automatic local or global correction

idea: fina a correct “nearby” program

try token insertions and deletions or exhaustive search

disadvantages: hard to implement,slows down parsing of correct programs, and “nearby” is not necessarily “the intended” program

the reason why creating this way:

past: slow recompilation cycle(even once a day) and find as many errors in one cycle as possible

present: quick recompilacation cycle, user tend to correct one error/cycle and complex error recovery is less compelling

Abstract syntax tree

Like parse trees but ignore some details

for instance:

parse tree

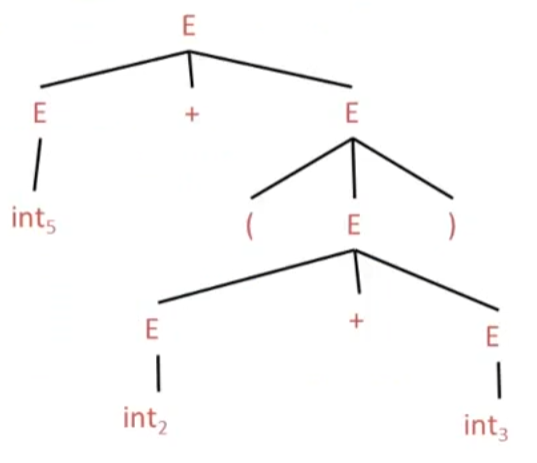
AST

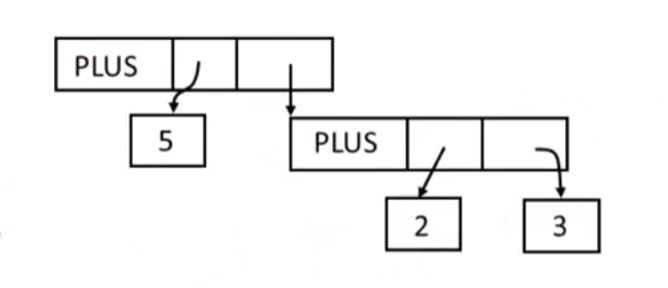
Recursive Descent Parsing

Algorithm

Let TOKEN be the type of tokens;

Let the global next point to the next input token;

Define boolean functions that check for a match of

a given token terminal:

1
bool term(TOKEN tok) {return *next++==tok;}

the nth production of S:

1
2
// check for the success of one production of S
bool Sn(){...}

all productions of S:

1
2
// check for the success of any productions of S
bool S(){...}

for instance:

Functions for start E:

a production: E -> T

1
bool E1(){return T();}

a production: E -> T + E

1
bool E1(){return T()&&term(PLUS)&&E();}

with backtracking’s E function

1
2
3
4
5
6
7
8
9
10
11
12
13
14
bool E(){
    /*
     * It saves the value of next into the save variable. 
     * This is done to be able to backtrack to the initial state for reattempting the match.
    */
    TOKEN *save=next;   
    /*
     * (next = save, E1()): It resets the value of next to save and then calls 
     * the function E1() to attempt to match the E1 expression. 
     * If E1 matches successfully, the entire expression returns true, 
     * and the next pointer is updated to the successful match position.
    */
    return (next=save,E1())||(next=save,E2());
}

Functions for non-terminal T:

a production: T -> int

1
bool T1(){return term(INT);}

a production: T -> int*T

1
bool T2(){return term(INT)&&term(TIMES)&&T();}

a production: T -> (E)

1
bool T3(){return term(OPEN)&&E()&&term(CLOSE);}

with backtracking’s T function:

1
2
3
4
bool T(){
    TOKEN *save=next;
    return {(next=save,T1())||(next=save,T2())||(next=save,T3());}
}

To start the parser:

Initialize next to point to first token and Invoke E()

Limitation

If a production for non-terminal X succeeds,cannot backtrack to try a different production for X later

Left recursion

for instance:

a production: S -> Sa

1
bool S1(){return S()&&term(a);}
1
bool S(){return S1();}

S() goes into an infinite loop

As a result, rewriting using right-recursion

for instance:

for (S -> Sa|b), we can rewrite it into (S -> bS’ and S’ -> aS’ | ɛ)

Predictive Parsing

Like recursive-descent but parser can “predict” which production to use

By looking at the next few tokens and no backtracking

Predictive Parsers accept LL(k) grammer (k = 1 always)

l:left-to-right scan l:left-most derivation k:k tokens look ahead

Parsing table Using

For the leftmost non-terminal S, we look at the next input token a, and choose the production shown at [S,a]

We use a stack to record frontier of parse tree:

  1. Non-terminals that have yet to be expanded

  2. Terminals that have yet to matched against the input

  3. Top of stack = lestmost pending terminal or non-terminal

Here is a pseudocode:

1
2
3
4
5
6
7
8
9
10
initialize stack = <S,$(end of input)> and next
repeat
    case stack of
        <X(non-terminal),rest>      :if T[X,*next] =  Y1...Yn 
                                        then stack <- <Y1...Yn, rest>;
                                        else error();
        <t(terminal),rest>          :if t == *next++
                                        then stack <- <rest>;
                                        else error()
until stack == <>

for instance:

Here is a parsing table:

int*+()$
ETXTX
X+Eɛɛ
TintY(E)
y*Tɛɛɛ

We can get the following table:

StackInputAction
E$int*int$TX
TX$int*int$intY
intYX$int*int$terminal
YX$*int$*T
*TX$int$terminal
TX$int$intY
intYX$int$terminal
YX$$ɛ
X$$ɛ
$$ɛ

First Sets

Assume non-terminal A,production A -> α, and token t

T[A,t] = α in two cases:

If  , we say that  

If    and    and    , we say that  

As a result,the first set’s definition is

Algorithm sketch:

  1. First(t)={t}

  2. · if  

    · if    and    for 1<=i<=n

  3.   if    and    for 1<=i<=n

for instance:

1
2
3
4
5
6
7
8
9
10
11
12
E -> TX         X -> +E|ɛ
T -> (E)|intY   Y -> *T|ɛ

First(()={(}
First())={)}
First(+)={+}
First(*)={*}
First(int)={int}
First(E)={(,int}
First(T)={(,int}
First(X)={+,ɛ}
First(Y)={*,ɛ}

Follow Sets

Definition: Follow(x)={}

If X -> AB then First(B)Follow(A) and Follow(X)Follow(B)

If    then Follow(X)Follow(A)

If S is the start symbol then  \subset$ Follow(S)

Algorithm sketch:

  1. \in$ Follow(S)

  2. First(β) - {ɛ}Follow(X) for each production A -> αXβ

  3. Follow(A)Follow(X) for each production A -> αXβ where ɛFirst(β)

for instance:

1
2
3
4
5
6
7
8
9
E -> TX         X -> +E|ɛ
T -> (E)|intY   Y -> *T|ɛ

Follow(E)=Follow(X)={$,)}     
Follow())=Follow(Y)=Follow(T)={+,$,)}  
Follow(()={(,int}
Follow(int)={*,+,$,)}
Follow(+)={(,int}
Follow(*)={(,int}

LL(1) Parsing table

Construct a parsing table T for CFG G

for each production A ->in G do:

for each terminalT[A,t] =

if, for eachdo: T[A,t] =

ifand\in Follow(A)] =

Note:

  1. If any entry is multiply defined then G is not LL(1)

  2. Most programming language CFGs are not LL(1)

Bottom-Up Parsing

Bottom-up parsers don’t need left-factored grammers

It reduces a string to the start symbol by inverting productions

Important Facts about bottom-up parsing:

  1. Tracing a rightmost derivation in reverse

  2. In shift-reduce parsing, handles appear only at the top of the stack,never inside

  3. For any grammer, the set of viable prefixes is a regular language

Shift-Reduce Parsing

Idea: split string into two substrings

Right substring is as yet unexamined by parsing; Left substring has terminals and non-terminals.The dividing point is marked by a “|”

Bottom-up parsers uses only two kinds of actions:shift and reduce

Shift: Move | one place to the right

Apply an inverse production at the right end of the left string

if A -> xy is a production,the Cbxy|ijk => CBA|ijk

the whole algorithm:

Left string can be implemented by a stack

Shift pushes a terminal on the stack

Reduce

  • pops 0 or more symbols off of the stack(production rhs)

  • pushes a non-terminal on the stack(production lhs)

Handles

Intuition:Want to reduce only if the result can still be reduced to the start symbol

Handles formalize the intuition: A handle is a reduction that also allows further reductions back to the start symbol

Recognizing Handles

There are no known effcient algorithms to recognize handles. However, there are good heyristics for guessing handles and on some CFGs, the heyristics always guess correctly

Viable prefix

  1. A viable prefix doesn’t extend past the right end of the handle

  2. As long as a parser has viable prefixes on the stack, no parsing error has been detected

Definition:

An item is a production with a “.” somewhere on the rhs

The only item for X -> ɛ is X -> .

eg. The items for T -> (E) are T -> .(E) , T -> (.E) , T -> (E.) , T -> (E).

The problem in recognizing viable prefixes is that the stack has only bits and pieces. These bits and pieces are always prefixes of rhs of productions

for instance:

consider the input (int)

E -> T+E | T

T -> int*T|int|(E)

Then (E|) is a state of a shift-reduce parse. (E is a prefix of the rhs of T-> (E)

Item T -> (E.) says that so far we have seen (E of this production and hope to see )

Idea: To recognize viable prefixes, we must recognize a sequence of partial rhs’s of productions,where each partial rhs can eventually reduce to part of the missing suffix of its predecessor

Algorithm:

  1. Add a dummy production S’ -> S to G

  2. The NFA states are the items of G(including the extra production)

  3. For item    add transition  

  4. For item    and    add  

  5. Every state is an accepting state

  6. Start state is S’ -> S

SLR Parsing

LR Parsing

Assume stack contains    , next input is t and DFA on input    terminates in state s

Reduce by    if s contains item  

Shift if s contains item   (s has a transition labeled t)

LR has a reduce/reduce conflict and shift/reduce conflict

SLR improves on LR shift/reduce heuristics --Few states have conflicts

SLR Parsing Algorithm

  1. Let M be DFA for viable prefixes of G

  2. Let  $   be initial configuration

  3. Repeat until configuration is S|$

  • Let    be current configuration

  • Run M on current stack  

  • If M accepts    with items I,let a be next input

    • Shift if  

    • Reduce if  and  

    • Report parsing error if neither applies

Improvements

Remember the state of the automaton on each prefix of the stack: <Symbol, DFA State>

Detail: The bottom of stack is <any, start> where any is any dummy symbol and start is the start state of the DFA

Define goto[i,A] = j if   

goto is just the transition function of the DFA

Define action table:

for each state    and terminal a

  • if    has item    and goto[i,a]=j then action[i,a]=shift j

  • if    has item    and    and X!=S’ then action[i,a]=reduce  

  • if    has item S’ -> S. then action[i,$]=accept

  • Otherwise, action[i,a]=error

Here is a SLR’s pseudocode:

1
2
3
4
5
6
7
8
9
10
11
12
let I=w$ be initial input
let j=0
let DFA state 1 have item S'->.S
let stack=<dummy,1>
    repeat
        case action[top_state(stack),I[j]] of
            shift k: push<I[j++],k>
            reduce X->A
                pop |A| pairs,
                push <X,goto[top_state(stack),X]>
            accept:halt normally
            error: halt and report error

Semantic Analysis

Scope

Matching identifier declarations with uses

Identifier Scope

The scope of an identifier is the portion of a program in which that identifier is accessible

The same identifier may refer to different things in different parts of the program

An identifier may have restricted scope

Static and Dynamic

Static Scope depends only on the program text, not run-time behavior

Dynamic Scope depends on execution of the program

A dynamically-scoped variable refers to the closest enclosing binding in the execution of the program

Not all identifiers follow the most-closely nested rule

Symbol Tables

Much of semantic analysis can be expressed as a recursive descent of an AST

Basic steps:

  • Before: process an AST node n

  • Recurse: process the children of n

  • After: finish processing the AST node n

for instance:

1
let x: Integer <- 0 in e

  • Before processing e, add definition of x to current definitions, overriding any other definition of x

  • Recurse

  • After processing e, remove definitions of x and restore old definition of x

A symbol table is a data structure that tracks the current bindings of identifiers

Symbol Tables’ definition and operations

For a simple symbol table we can use a stack

Operations:

  1. add_symbol(x): push x and associated info on the stack

  2. find_symbol(x): search stack, starting from top, for x. Return first x found or NULL if not found

  3. remove_symbol(): pop the stack

However,we will meet the problem of function scope

1
f(x:Integer, x:Integer, ...)

revised operations:

  1. enter_scope(): start a new nested scope

  2. find_symbol(x): finds current x (or null)

  3. add_symbol(x): add a symbol x to the table

  4. check_scope(x): true if x defined in current scope

  5. exit_scope(): exit current scope

Multiple passes

If class names can be used before being defined,we requires multiple passes

Pass 1: Gather all class names

Pass 2: Do the checking

Type

The goal of type checking is to ensure taht operations are used with the correct types

Type Checking: the process of verifying fully typed programs

Type Inference: the process of filling in missing type information

The kinds of Type

Statically typed: All or almost all checking of types is done as part of compilation

Dynamically typed: Almost all checking of types is done as part of program execution

Untyped: No type checking

Type Checking

Building blocks

  • Symbolis “and”

  • Symbol => is “if-then”

  • x:T is “x has type T”

Tradition inference rules are written:

means “it is provable that …”

A type system is sound if whenever, then e evaluates to a value of type

Type checking proves facts e: T

  • Proof is on the structure of the AST

  • Proof has the shape of the AST

  • One type rule is used for each AST node

In the type rule used for a node e:

  • Hypotheses are the proofs of types of e’s subexpressions

  • Conclusion is the type of e

Types are computed in a bottom-up pass over the AST

Type Environments

A type environment gives types for free variables. It is a function from ObjectIdentifier to Types. A variable is free in an expression if it isn’t defined within the expression

Let O be a function from ObjectIdentifier to Types, the sentencemeans that under the assumption that variables have the types given by O, it is provable that the expression e has the type T

Subtype

Define a relationon classes

  • XX

  • XY if X inherits from Y

  • XZ if XY and YZ

Runtime

Runtime Organization

When a program is invoked:

  • The OS allocates space for the program

  • The code is loaded into part of the space

  • The OS jumps to the entry point (i.e., “main”)

Activations

Definition

An invocation of procedure P is an activation of P

The lifetime of an activation of P is all the steps to execute P. (Including all the steps in procedures P calls)

The lifetime of a variable x is the portion of execution in which x is defined

Note that

Lifetime is a dynamic (run-time) concept

Scope is a static concept

Activation Records

The information needed to manage one procedure activation is called an activation record or frame

The compiler must determine, at compile-time, the layout of activation records and generate code thatcorrectly accesses locations in the activation record. Thus, the AR layout and the code generator must bedesigned together!

Globals & Heap

All references to a global variable point to the same object

Globals are assigned a fixed address once

Depending on the language, there may be other statically allocated values

Languages with dynamically allocated data use a heap to store dynamic data

1
2
3
4
5
6
7
8
9
10
11
---------------------   Low Address
|       Code        |
---------------------
|    Static Data    |
---------------------
|       Stack       |
----------↓----------
|                   |
----------↑---------
|       Heap        |
---------------------   High Address

The code area contains object code. For many languages,fixed size and read only.

The static area contains data (not code) with fixed addressed(e.g., global data)

The stack contains an AR for each currently active procedure. Each AR usually fixed size, contains locals

Heap contains all other data

Both the heap and stack grow. We must take care that they don’t grow into each other

Solution: start heap and stack at opposite ends of memory and let them grow towards each other

Alignment

Most modern machines are 32 or 64 bit

  • 8 bits in a byte

  • 4 or 8 bytes in a word

  • Machines are either byte or word addressable

Data is word aligned if it begins at a word boundary

Most machines have some alignment restrictions or performance penalties for poor alignment

Stack Machines

Only storage is a stack

An instruction r =

  • Pops n operands from the stack

  • Computes the operation F using the operands

  • Pushes the result r on stack

Location of the operands/result is not explicitly stated because they always at the top of stack

Code Generation

Two assumptions:

  1. Execution is sequential; control moves from one point in a program to another in a well-defined order

  2. When a procedure is called, control always returns to the point immediately after the call

Optimization

When should we perform optimizations?

On AST:

Pro: Machine independent

Con: Too high level

On assembly language:

Pro: Exposes optimization opportunities

Con: Machine dependent

Con: Must reimplement optimizations when retargeting

On an intermediate language

Pro: Machine independent

Pro: Exposes optimization opportunities

Basic Block

A basic block is a maximal sequence of instructions with no labels(except at the first instruction) and no jumps(except in the last instruction)

Idea:

  • Cannot jump into a basic block(except at beginning)

  • Cannot jump out of a basic block(expect at end)

  • A basic block is a single-entry, single-exit, straight-line code segment

Control-flow Graph

A control-flow graph is a directed graph with

  • Basic blocks as nodes

  • An edge from block A to block B if the execution can pass from the last instruction in A to the first instruction in B

    • for instance: the last instruction in A is jump

    • for instance: execution can fall-through from block A to block B

The body of a method (or procedure) can be represented as a control-flow graph

There is one initial node and all “return” nodes are terminal

Local Optimization

Algebra simplification

for instance:

x:=x*0 => x:=0

y:=y**2 => y:=y*y

x:=x*8 => x:=x<<3

x:=x*15 => t:=x<<4;x:=t-x

Constant merge

Operations on constants can be computed at compile time

If there is a statement x:=y op z, y and z are constants then y op z can be computed at compile time

for instance: x:=2+2 => x:=4

Constant folding can be dangerous for cross-complier

1
2
3
4
5
6
Compiler    ------>     Gen Code(week machine)
---------               ---------
|       |               |       |
|   X   |               |   Y   |
|       |               |       |
---------               ---------

X and Y are different ​architectures

Dead Code Elimination

Eliminate unreachable basic blocks:Code that is unreachable from the initial block

Removing unreachable code makes the program smaller

Peephole Optimization

Optimizations can be directly applied to assembly code. Peephole optimization is effective for improving assembly code

The “peephole” is a short sequence of (usually contiguous) instructions

The optimizer replaces the sequence with another equivalent one (but faster)